Mathematics Program and Computer Science Program Present

Using Continuous Results in Discrete Problems

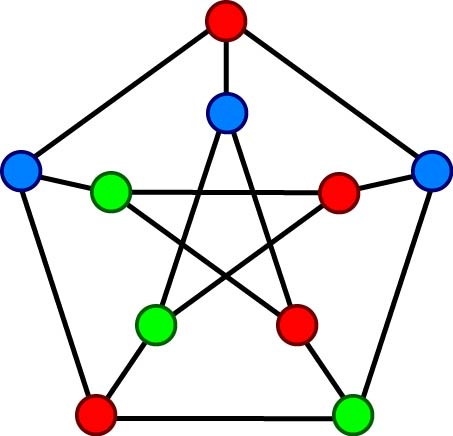
Often, continuous and discrete are treated as opposites of each other. The Borsuk--Ulam theorem states that for any continuous map  from the sphere to Euclidean space, $fcolon S^dto R^d$, there is a pair of antipodal points that are identified, so $f(x)=f(-x)$. This theorem deals with continuous objects, is fundamentally topological, and yet, it has numerous applications to discrete results. We will look at how these methods apply to some problems, including chromatic numbers of Kneser graphs (like the Petersen graph which you see pictured) and the Ham Sandwich theorem: given a $d$-dimensional sandwich with $d$ ingredients, with a single cut you can split your sandwich in half such that every ingredient is exactly halved as well. We will also look at what it means to take a colorful generalization of a result and why it is helpful.

---

For more information, call 845-758-6822, or e-mail [email protected].

Time: 12:00 pm – 1:00 pm EST/GMT-5

Location: RKC 111

Subscribe: Save this Event: Subscribe / .ics File